State machines are a really nice way of thinking about systems with state. As a notation for expressing imperative code, I much prefer this:
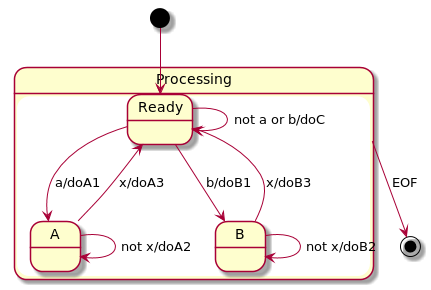
To this:
x = readchar();
while(x != EOF) {
if(x == 'a') {
doA1();
x = readchar();
while(x != EOF && x != 'x') {
doA2(x);
x = readchar();
}
doA3();
} else if (x == 'b') {
doB1();
x = readchar();
while(x != EOF && x != 'x') {
doB2(x);
x = readchar();
}
doB3();
} else {
doC();
x = readchar();
}
}
I've always wished I could write that sort of code as a state machine rather than a bunch of nested structured programming primitives. Although there is some charm to the idea of drawing a diagram on the computer and having that be compiled as executable code, though, that can also be fiddly and isn't well supported by conventional programming tools; so I'd rather actually describe my state machine in text. What I want is a syntax for writing state machines, rather than writing imperative code that implements the state machine.
For instance, the diagram I put above wasn't drawn by me; it was drawn by a tool called PlantUML from the following source code:
@startuml
state Processing {
Ready --> A : a/doA1
Ready --> B : b/doB1
Ready --> Ready : not a or b/doC
A --> A : not x/doA2
A --> Ready : x/doA3
B --> B : not x/doB2
B --> Ready : x/doB3
}
[*] --> Ready
Processing --> [*] : EOF
@enduml
But the UML state diagram is meant for abstract modelling of systems, and lacks the precision and detail required for actual executable code. The state diagram doesn't make it clear that doA2 and doB2 need to be passed the character that was read, for instance. PlantUML's syntax, therefore, also lacks that kind of detail, so we can't just use that.
Also, in a programming situation, it would be nice to be able to express types of state machines: to be able to say that a group of state machines has some useful properties in common, defined by the "type". The type of a state machine defines some high-level states and what inputs or outputs are possible in each state; any state machine of that type has to follow that behaviour, even though it might break the states defined in the type into many substates. For instance, the example state machine above always accepts any character until it receives an EOF, then stops; that might be expressed as a type having a single Ready state with two transitions, one mapping an EOF to the end state and another mapping a character back to the Ready state, with no outputs. That type would be suitable for any state machine that accepts characters until they finish, so a generic "character input stream" might accept a state machine of that type to process them, without needing to know anything about As and Bs.
These thoughts have led me to the following model of a state machine that's suitable for use as part of a programming language (although I've not defined an actual syntax yet):
State machine type
A state machine type is a set of states. Each state has a name, and a list of message types which are acceptable in that state (I am assuming that the underlying type system is smart enough to include things like "character equal to a" as a type, rather than merely "character"). This list must be disjoint.
For each input message type, there's a list of possible next states and an output message type (which in our example above would be a void type, as we never output messages).
There is also an initial state. It's impossible for the initial state to be the target of a state transition on a message, so it only has transitions out to other states. Those transitions all represent possible constructors of this state machine, because the initial state represents nonexistance.
For instance, a type" for vending machine controller state machines might be (given a Result type which has two values, success and fail):
Initial state:
input: (Create) output: (Void) next state: (Idle)
Idle state:
input: (Coin(Value)) output: (Value) next state: (Credit)
Credit state:
input: (Coin(Value)) output: (Value) next state: (Credit)
input: (Refund) output: (Value) next state: (Idle)
input: (Select(Product)) output: (success::Result) next state: (Idle)
input: (Select(Product)) output: (fail::Result) next state: (Credit)
The Value objects output in response to Coin or Refund inputs happen to reflect the current credit in the machine, a fact which the state machine type alone can't represent (that would need to be explained in a design-by-contract invariant of some kind).
From this type can be derived the type of the state machine's transition functions, which in this case will be:
coin :: Idle -> Value -> (Credit,Value) |
Credit -> Value -> (Credit,Value)
refund :: Credit -> (Idle,Value)
select :: Credit -> Product -> (success::Result,Idle)|(fail::Result,Credit)
Note that the Create transition isn't represented here, because this state machine can't actually be instantiated - it doesn't specify the behaviour enough. There's no way of saying which possible select result should happen, or of what values are returned as outputs. But the functions we have are automatically implemented by the state transition definition, and will cause the appropriate transitions to occur in any state machine that's a subtype of this one; every function accepts an instance of the state machine in a given state, and an input value, and returns a new instance of the state machine and the output value.
Subtyping
State machine types can be subtypes of other state machine types.
A state in the parent type may be split into several states in the subtype; any transition to a state A in the parent type must be represented by a transition in the subtype to some substate of A, and all transitions possible from state A in the parent type must be represented by transitions from every substate of A in the child.
For instance, a subtype of the vending state machine might have an infinite number of substates of "Idle", one for each possible configuration of available things to vend inside the machine. If it vends three different products, then these substates might be called Idle(A,B,C) where A,B and C are nonnegative integers representing the stock of each item. The only transition out of "Idle" is when a coin is inserted, so every Idle(A,B,C) state must have a transition from a coin being inserted, returning a Value, and taking us into the Credit state.
However, our Credit state also tracks the stock, and also tracks the credit inserted so far - so we need an infinite set of states of the form Credit(A,B,C,X) where A,B,C are the stocks and X is another nonnegative integer for the number of pennies of credit. So the parent-type transition from Idle to Credit has to be replaced by a transition from every Idle(A,B,C) to Credit(A,B,C,X) where X is the Value of the coin inserted. All the transitions from Credit in the parent type need to be represented as transitions from every Credit(A,B,C,X) state to other Credit(A,B,C,X) or Idle(A,B,C) types as appropriate. But with that done, it can be shown that all the states and transitions of the parent type correspond to one or more in the subtype.
The one exception is the initial state - the creation transitions from that in the subtype need not correspond to those of the parent type.
Given an extension to the syntax to create "parameterised states" such as Idle(A,B,C), which are shorthand for a potentially infinite set of "concrete states" such as "Idle(4,0,1)", we might represent that subtype like so:
Initial state:
input: (Create(a::NonNegativeInteger,b::NonNegativeInteger,c::NonNegativeInteger))
output: (Void) next state: (Idle(A,B,C))
Idle(a::NonNegativeInteger,b::NonNegativeInteger,c::NonNegativeInteger)
state implements Idle:
input: (Coin(x::Value)) output: (x::Value) next state: (Credit(a,b,c,x))
Credit(a::NonNegativeInteger,b::NonNegativeInteger,c::NonNegativeInteger,x::NonNegativeInteger)
state implements Credit:
input: (Coin(x'::Value)) output: ((x+x')::Value) next state: (Credit(a,b,c,x+x'))
input: (Refund) output: (x::Value) next state: (Idle(a,b,c))
input: (Select(Product==A)) when: a>0 output: (Success) next state: (Idle(a-1,b,c))
input: (Select(Product==A)) when: a==0 output: (Fail) next state: (Credit(a,b,c,x))
input: (Select(Product==B)) when: b>0 output: (Success) next state: (Idle(a,b-1,c))
input: (Select(Product==B)) when: b==0 output: (Fail) next state: (Credit(a,b,c,x))
input: (Select(Product==C)) when: c>0 output: (Success) next state: (Idle(a,b,c-1))
input: (Select(Product==C)) when: c==0 output: (Fail) next state: (Credit(a,b,c,x))
(We really should have represented the stock as a Map(Product,NonNegativeInteger) type and then not duplicated the select rules...)
Converting a parent state into a parameterised subtype state is only one way of splitting a state in a subtype, too. The syntax above would permit the creation of separate states that all say "implements Credit", too. A very simple vending machine that can only hold one instance of one product might split Idle into two states, Empty and Full, for instance; and probably split Credit into CreditFull(Value) and CreditEmpty(Value) to represent the Credit state while also parameterising CreditFull and CreditEmpty with the current credit.
The above syntax for parameterised states can get unweildy if there's a lot of parameters, especially if generally only a few of them are changed in any given transition (imagine the above example of there were ten different products to keep track of). Therefore, as syntactic sugar, it makes sense for it to be possible to define parameters shared implicitly by one or more states. Transitions into those states from states outside the group need to explicitly specify all the parameter values, but transitions within that group can use a different syntax to represent the next state, which only specifies what parameters have changed. All the rest are passed in unchanged, automatically. It might look like this:
Initial state:
input: (Create(a::NonNegativeInteger,b::NonNegativeInteger,c::NonNegativeInteger))
output: (Void)
next state: (Idle(A,B,C))
parameters a::NonNegativeInteger,b::NonNegativeInteger,c::NonNegativeInteger {
Idle(a,b,c) state implements Idle:
input: (Coin(x'::Value)) output: (x'::Value) next state: (Credit(x <- x'))
Credit(a,b,c,x::NonNegativeInteger) state implements Credit:
input: (Coin(x'::Value)) output: ((x+x')::Value) next state: (Credit(x <- x+x'))
input: (Refund) output: (x::Value) next state: (Idle())
input: (Select(Product==A)) when: a>0 output: (Success) next state: (Idle(a <- a-1))
input: (Select(Product==A)) when: a==0 output: (Fail) next state: (Credit())
input: (Select(Product==B)) when: b>0 output: (Success) next state: (Idle(b <- b-1))
input: (Select(Product==B)) when: b==0 output: (Fail) next state: (Credit())
input: (Select(Product==C)) when: c>0 output: (Success) next state: (Idle(c <- c-1))
input: (Select(Product==C)) when: c==0 output: (Fail) next state: (Credit())
}
Implementing state machine types
Note that we've suddenly started giving names to the Values flying around, and specifying an output value rather than just a type, and splitting transitions into different cases with disjoint boolean "when:" expressions. This, too, further constrains the type of the state machine; indeed, this machine can actually be implemented and will provide a simple model of a vending machine - although nothing will be vended.
This means that this new state machine's state transition functions will include a "create" function from the initial stock levels to an instance of Idle(NonNegativeInteger,NonNegativeInteger,NonNegativeInteger).
A real implementation could further subtype this, adding a uniquely-typed IO interface to the Idle and Credit states, passed into the create transition. The Success-returning select operations can then also use pure IO functions to mutate the IO context to one in which the physical mechanism of vending has happened.
But the implementation of a state machine exists in the expressions that return the output value, parameterise the next state, and the boolean expressions forming the "when:" guards. These are full expressions in the pure functional language I'm imagining this thing implemented on top of, so are fully Turing complete.
There is no syntactic distinction between a type and an implementation; a state machine type can be instantiated if all of its outputs have expressions giving them values (ok, singleton-typed outputs such as Void can be implied!). This is a bit like concrete versus abstract classes in an object-oriented programming language.
Chaining transitions
So far, we've only looked at transitions that accept an input value, return an output value and move to a new state. This means that state machine behaviour is defined entirely in terms of its reactions to external values. Since the values we generate for the output and the parameters of the new state are Turing-complete expressions, that is sufficient to describe any behaviour, but it's not always convenient to express complicated behaviour in an expression. Sometimes a complicated operation of a compound data structure such as a list would be better defined as a state machine in its own right.
In order to support that kind of thing, we can also support chaining transitions, which can drive state machine behaviour purely based on internal state, and so do not cause the generation of state transition functions. These come in three types.
The first kind is one that starts with an input value, but which then leads to a next state without producing a value. This next state must be a special "transient state", the rules for which are explained below.
The second kind is one from a transient state to another transient state. This has no input value and no output value.
The third kind is a transition from a transient state to a non-transient state, which produces an output value.
Transient states may not have any non-chaining transitions point to and from them. Every transient state must be referenced from at least one non-transient state through a chain of chaining transitions, starting with a kind-1 chaining transition then zero or more kind-2 chaining transitions. Every transient state must also lead to at least one non-transient state through a chain of zero or more kind-2 chaining transitions, then a kind-3 chaining transition.
Every such possible chain from a kind-1, through zero or more kind-2, to a final kind-3, is equivalent to a single transition from the initial to the final non-transient states; with the kind-1 transition defining the input value and the kind-3 transition defining the output value. They might be implemented as a set of state-transition functions that just tail-call each other, but
the transient states are therefore "hidden" inside the state machine from external perspectives. Those state-transition functions are lexically local to the exposed state-transition functions implementing the equivalent non-chaining transition.
But although they are hidden from users of the state machine, a subtype of the state machine can indeed "see" them for purposes of splitting them into substates, adding transitions between them, etc.
Termination
The final thing I've not covered above is terminating state machines. There's an implicit "final" state available in every state machine, if at least one transition to it exists; no transitions from that state can exist. Any transition to the final state appears in the state transition functions as a function that returns the output value, but not paired with a new state machine instance, because there isn't one. It's gone.
It is entirely possible for a state machine to have no non-transient states apart from the initial and final states. For instance, a state machine that traverses a tree and sums up the labels on the nodes might be implemented in terms of transient parameterised states for the current position in the tree and the running total, with an kind-1 creation transition that accepts the tree as an input and a kind-3 finalisation transition that returns the count. This machine will therefore have a single state transition function - from Tree to Number. The actual state of the machine is entirely represented as state parameters passed between mutually recursive functions implementing the chaining transitions, and never appears as a value visible outside of that.
Conclusion
I think I've defined a workable semantic model for state machines that can be used as a way to define sets of pure functions between instances of state machines, that can handle both synchronous state machines driven by external events, and those that bumble around a data structure or iterate mathematical operations.
It needs a proper syntax; personally, I'd prefer one based on s-expressions or IRON, but suitably consistent forms could be defined for any language.












